Per expressar les relacions entre una acció i una altra, hi ha uns
quants dibuixets internacionals. Els operadors bàsics que has de conèixer
són 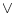 ,
, 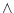 ,
, 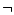 ,
, 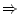 . Els altres són més
complicats, però els he posat tots per quan hagis de consultar-los.
. Els altres són més
complicats, però els he posat tots per quan hagis de consultar-los.
| Símbol |
Llegit... |
Descripció |
|---|
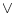 |
o |
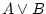 es compleix quan un dels dos, o tots dos, és cert. es compleix quan un dels dos, o tots dos, és cert. |
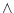 |
i |
Per a què 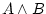 es compleixi, tant es compleixi, tant 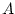 com com 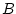 han de ser
certs. han de ser
certs. |
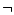 |
no |
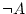 només es compleix quan només es compleix quan 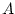 és fals. és fals. |
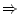 |
implica |
Indica una conseqüència. La expressió
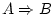 diu que quan diu que quan
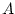 es compleix, llavors es compleix, llavors 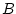 també. A més, també. A més,
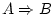 és
cert excepte pel cas és
cert excepte pel cas 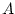 cert i cert i 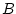 fals. Per entendre-ho, pensa
en un fals. Per entendre-ho, pensa
en un 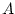 que impliqui que impliqui 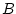 i pregunta't: és possible que i pregunta't: és possible que 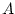 sigui cert i
sigui cert i 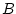 no? Tampoc et preocupis molt per això, no és important
ara. no? Tampoc et preocupis molt per això, no és important
ara. |
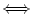 |
si i només si |
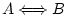 equival a equival a
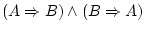 .
Vol dir que de .
Vol dir que de 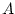 podem deduir podem deduir 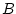 i viceversa, o sigui, que són
equivalents. i viceversa, o sigui, que són
equivalents. |
 |
fals |
El quadradet buit representa a fals (el 0 binari). Més
tècnicament, representa a 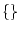 . . |
 |
cert |
El quadradet ple representa a cert (l'1 binari). Més
tècnicament, representa a 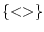 . . |
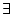 |
existeix... |
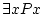 es llegeix existeix un es llegeix existeix un 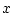 tal que tal que 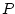 de de 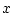 .
Si al nostre domini podem trobar un element (o més) tal que es compleixi
la propietat .
Si al nostre domini podem trobar un element (o més) tal que es compleixi
la propietat 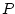 aplicada a aquest element, llavors la fórmula és
certa. aplicada a aquest element, llavors la fórmula és
certa. |
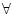 |
per tot... |
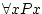 es llegeix per tot es llegeix per tot 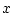 , , 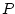 de de 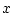 . Si tots
els elements amb què treballem compleixen la propietat . Si tots
els elements amb què treballem compleixen la propietat 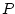 , llavors
la fórmula és certa. , llavors
la fórmula és certa. |
 |
llavors |
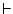 és el símbol del seqüent, que és la manera de dir
``quan es compleix tot això de l'esquerra passa també tot
allò de la dreta''. Hi ha seqüents vàlids, com és el símbol del seqüent, que és la manera de dir
``quan es compleix tot això de l'esquerra passa també tot
allò de la dreta''. Hi ha seqüents vàlids, com
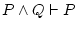 o com
o com
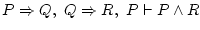 . També
n'hi ha d'invàlids, com . També
n'hi ha d'invàlids, com
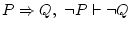 . L'objectiu
de la deducció natural és demostrar que un seqüent és vàlid. . L'objectiu
de la deducció natural és demostrar que un seqüent és vàlid. |
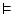 |
vàlid |
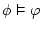 serveix per dir que serveix per dir que 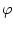 és conseqüència
lògica de és conseqüència
lògica de 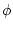 , però quan s'escriu , però quan s'escriu 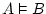 , es vol dir que
el seqüent , es vol dir que
el seqüent 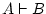 és vàlid; o sigui, que hem pogut demostrar-ho
d'alguna manera, i ara es considera cert sota qualsevol interpretació
dels símbols de predicat. és vàlid; o sigui, que hem pogut demostrar-ho
d'alguna manera, i ara es considera cert sota qualsevol interpretació
dels símbols de predicat. |
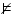 |
invàlid |
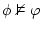 vol dir que vol dir que 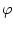 no és conseqüència lògica
de no és conseqüència lògica
de 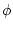 . Si trobes una sèrie de valors (model) que faci
cert a . Si trobes una sèrie de valors (model) que faci
cert a 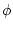 però fals a però fals a 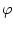 , es demostra la invalidesa. , es demostra la invalidesa. |
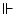 |
satisfactible |
Un conjunt de fórmules és satisfactible si existeix una sèrie de valors
(model) que les faci certes a totes al mateix temps. |
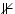 |
insatisfactible |
Un conjunt de fórmules és insatisfactible si no hi ha cap combinació
de variables (model) que les faci totes certes al mateix temps. |
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Els altres són més
complicats, però els he posat tots per quan hagis de consultar-los.
. Els altres són més
complicats, però els he posat tots per quan hagis de consultar-los.