5.7 Iu kun provo per okazoj. $P\vee(Q\wedge R)\vdash P\vee Q$

Oni uzu la plej malfacilan derivregulon, elaŭigon. $P\vee(Q\wedge R)\vdash P\vee Q$ solvita:

$$\begin{fitch} \par P \vee (Q \wedge R) \\ \par \fh P & H \\ ... ...I$\vee$\ 5 \\ \par P \vee Q & E$\vee$\ 1,3,6 \par \end{fitch}$$

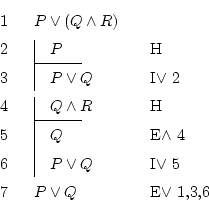
Vi jam scias la regulojn, do mi klarigas la manieron pensi de iu homo, kiu eble ne komprenas naturan dedukton, sed estas iom pensema:

Oni devas pruvi ke $P\vee Q$ ĉiam certas. La maldekstra esprimo, $P\vee(Q\wedge R)$, povas certiĝi pro du motivoj:

• se ĝi certas pro la vero de $P$, tiam $P\vee Q$ ja estas certa.
• se ĝi certas pro la vero de $Q\wedge R$, tiam $Q$ kaj $R$ estas ambaŭ certaj, do $P\vee Q$ certas per $Q$.

Do, ĉiel, $P\vee Q$ estas vera.

Nun, la cetero estas traduki tion al logika lingvo, sekvante la saman ordon kiel antaŭe, kaj iom post iom.

Oni komencas pruvante unu vojo, poste, la alian, kaj fine oni aplikas elaŭigon. Por klarigi la regulon oni devas skribi la linion kiu enhavas la disjunkcion, kaj la du liniojn el ene de ĉiu subderivo kie montriĝas ke, supozante iun aĵon aŭ la alian, la rezulto estas la samo.

Rimarku ke, eĉ se oni eltrovis ke $P\Rightarrow P\vee Q$ kaj ke $Q\wedge R\Rightarrow P\vee Q$, ne estas necese uzi kunimplikaciigon por restigi skribe tion.

La plej malfacilo el la provo per okazoj normale estas decidi, kiun esprimon oni provos pruvi en ambaŭ okazoj. Ĝi estu la sama en ambaŭ okazoj!