5.1 Iu tre simpla. $P,\ P\Rightarrow Q\vdash P\wedge Q$

La solvo al $P,\ P\Rightarrow Q\vdash P\wedge Q$ estas:

$$\begin{fitch} \par P \\ \par P \Rightarrow Q \\ \par Q & E$... ...ow$\ 2,1 \\ \par P \wedge Q & I$\wedge$\ 1,3 \par \end{fitch}$$

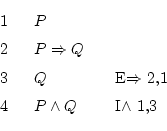
Jen oni ne devas tro pensadi, nur devas bone uzi la regulojn kaj iliajn klarigojn.

Unue, komprenu kion ni estis demandita: oni diras ke nun okazas du aĵojn, la unua estas $P$ kaj la dua $P\Rightarrow Q$ (ili estas la du formulojn verkitajn maldekstre de la simbolo $\vdash$). Ĉi tiujn oni devas noti, unu po linio, ĉar ĉe tiu derivo, ili estos ĉiam certaj (tion ŝatante aŭ ne).

La celo de tiu derivo estas sciiĝi ke $P\wedge Q$ ankaŭ certas, ĉar oni aldiris ke kiam $P$ kaj $P\Rightarrow Q$ estas certaj, tiam $P\wedge Q$ ankaŭ estas vera, kaj ni volas pruvi ke tio estas prava. Videble, oni fine atingis tion, ĉar en la lasta linio estas verkita formulo $P\wedge Q$.

Nu, kiel ni sekvos? Oni devas ekscii al kie oni volas aliri. Se $P\wedge Q$ devas certi, tiam ambaŭ $P$ kaj $Q$ devos certi; do oni okupu por pruvi ke ili ja certas.

$P$ certas, ĉar estas fakto dirite al ni komence; ĝi estas skribita en linio 1.

Sed neniu diris al ni ke $Q$ ankaŭ certu. Kion oni diris pri $Q$? Serĉinte ĝin en linioj 1 kaj 2, oni nur konas ke $Q$ certas kiam $P$ okazas (tion diras la linio 2). Sed $P$ ja estas vera, do oni povas uzi unu el la reguloj por dedukti $Q$ el $P\Rightarrow Q$ kaj $P$. Rimarku la plej gravan ŝanĝon ĉe la transformo de $P\Rightarrow Q$ al $Q$: ĉe la dua formulo, implikacion simbolon oni ne jam uzis; do regulo kiun oni bezonas estas la nomata forigo de implikacio, aŭ elimplikaciigo.

Por uzi tiun derivregulon, oni konsultas ĝian difinon, kaj eltrovas ke en novan linion oni devas meti la $Q$, kaj kiel klarigo $E\Rightarrow\ 2,1$ estu skribita dekstre. La $E$ estas pro la angla elimination (aŭ la esperanta el-), la $\Rightarrow$ estas pro implikacio, la unua numero estas tiu el la linio kiu enhavas implikacion ( $P\Rightarrow Q$), kaj la dua numero, el la linio kiu diras la konatan veraĵon ($P$). Estus malkorekte metu ilin turnite ( $E\Rightarrow\ 1,2$), ĉar la difino de la regulo esprimas ke linio kiu havas la implikacion estu citita unue.

Jam aplikite la regulon, oni scias tri veraĵojn: ke $P$, ke $P\Rightarrow Q$, kaj ke $Q$. Ĉiuj estas same certaj. Nun ni estas pli proksime al nia celo, $P\wedge Q$, ĉar ni ja scias ke $P$ kaj $Q$ estas veraĵoj, do $P\wedge Q$ ankaŭ devas esti (memvideble). Ĉe la formulo ni serĉadas estas signo de konjunkcio ($\wedge$) kiun oni mankas, do uzu kunkajigon (longe nomata enigo de konjunkcio) por ebligi aserti ke $P\wedge Q$ pravas ĉar $P$ certas kaj $Q$ same. Kiel klarigo oni metas $I\wedge\ 1,3$ (linio kiu diras ke $P$, kaj tiu kiu diras ke $Q$). Ne eblas meti $I\wedge\ 3,1$; tio estus por aserti $Q\wedge P$, kio ne estas nia pruvenda formulo.

Tiam jam scias 4 certajn aĵojn: $P$, $P\Rightarrow Q$, $Q$, kaj $P\wedge Q$. Eblas daŭrigi nian eltrovadon de veraĵoj, sed ni jam finiĝis, ĉar oni demandis al ni pruvi la verecon de $P\wedge Q$, kaj oni jam atingis ĝin (ĉe linio 4). Do, tiu estos la lasta linio, kaj oni ne devas plu skribi.

Ha, jen ĉi tiu ekzemplo pervorte: ``ĉi tiam estas somero, kaj ĉe somero estas varma. Do, ĉi tiam estas somero kaj estas varma''.