5.13 I had this one in an exam. $A\vee B,\ A\Rightarrow C,\ \neg D\Rightarrow\neg B\vdash C\vee D$

In the final exam of ILO they were asking $A\vee B,\ A\Rightarrow C,\ \neg D\Rightarrow\neg B\vdash C\vee D$, and I needed a very very long time until I got it:

$$\begin{fitch} \par A \vee B \\ \par A \Rightarrow C \\ \par... ...\vee$\ 12 \\ \par C \vee D & E$\vee$\ 1,6,13 \par \end{fitch}$$

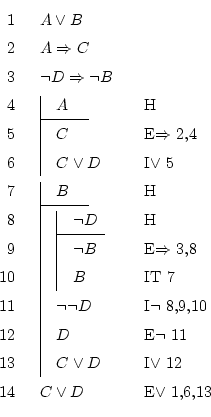
Remark that the result we're searching, $C\vee D$, is a disjunction. Since you already know the disjunction introduction, you could simply search $C$, and then use that rule to get $C\vee D$. Or if with $C$ didn't work, you could try with $D$, since if $D$ is true, then $C\vee D$ also is, and we're done.

Unfortunately, $C$ is not always true, and $D$ also isn't always true (on the other hand, $C\vee D$ is always true, and that's what we're trying to prove). After seeing this, we must search another method which works with the two formulas, $C$ and $D$, at the same time, since it seems that if we take only one without looking at the other, then it does not provide much information.

To use the $A\vee B$ we must use proof by cases. We will try to see that both $A$ and $B$ lead to $C\vee D$, since if we can do that, we will have finished.

$A$ implies $C$, and if $C$ is true then $C\vee D$ also is, so $A$ implies $C\vee D$.

With $B$, what we know doesn't relate it to $C$ but to $D$. We want $C\vee D$. Hardly we will make true $C\vee D$ because of $C$, so we will try to make true just the $D$. To do so, we will use reduction to the absurd: suppose that $D$ is false, then it holds that $\neg B$ thanks to the formula on line 3. But we were under the supposition that $B$ was true, so our hypothesis $\neg D$ can't be true, thus $D$ is true, and so is $C\vee D$.

Since $A\vee B$ is true, and both paths lead to $C\vee D$, we finally see that $C\vee D$ is always true.

If you are skilled working with logical formulas, you will have seen that $\neg D\Rightarrow\neg B$ is $B\Rightarrow D$. This simplifies the problem and helps understanding it faster. But anyway, you can't change $\neg D\Rightarrow\neg B$ to $B\Rightarrow D$ directly, you would have to do it step by step.