5.12 An interesting one. $P\vee Q,\ \neg P\vdash Q$

Another which seems easy: $P\vee Q,\ \neg P\vdash Q$. Let's see:

$$\begin{fitch} \par P \vee Q \\ \par \neg P \\ \par \fh P & ... ...par \fa Q & IT 9 \\ \par Q & E$\vee$\ 1,8,10 \par \end{fitch}$$

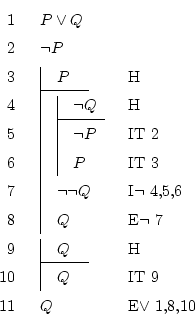
It's very easy to understand by anyone: it holds $P\vee Q$, but $P$ is false, so the truth is $Q$.

It can be done in several ways, but at some time you will have to use disjunction elimination to do something with the $P\vee Q$. We're going to prove that both $P$ and $Q$ lead to the same place, which will be our target formula $Q$ (since it's possible, let's go directly for $Q$).

We open subdemonstration supposing that $P$, and we must see that $Q$. It isn't too hard since we have $\neg P$ on line 2; this helps contradicting anything we want. Since what we're searching is $Q$, we suppose $\neg Q$ and by reduction to the absurd we obtain $\neg\neg Q$, which is $Q$.

The other path, when we suppose $Q$ true, leads us directly to $Q$.

In conclusion, both paths go to $Q$ and by disjunction elimination we get the proof that $Q$ is always certain.