5.10 Suppose the contrary. $\vdash\neg(P\wedge\neg P)$

Another simple one, $\vdash\neg(P\wedge\neg P)$. It's done this way:

$$\begin{fitch} \par \fh P \wedge \neg P & H \\ \par \fa P & E... ...\ \par \neg (P \wedge \neg P) & I$\neg$\ 1,2 \par \end{fitch}$$

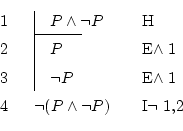
We all know that two contrary things can't happen at the same time, but, how can this be proved? We must use the reduction to the absurd:

Suppose that it does happen $P\wedge\neg P$. Then happen both $P$ and $\neg P$, both at the same time, which is a contradiction. So, the supposition we just done can't be true: it's false. This way we can prove $\neg(P\wedge\neg P)$.

When you see something so clear and obvious as $\neg(P\wedge\neg P)$, then its contrary will be clearly false and absurd. So, it won't be too difficult to see that it doesn't hold and that it contradicts itself. Once done, we can assure that the original formula is true since its contrary is false.