5.9 Left side empty. $\vdash P\Rightarrow P$

Proving $\vdash P\Rightarrow P$ is very easy and short:

$$\begin{fitch} \par \fh P & H \\ \par \fa P & IT 1 \\ \par P \Rightarrow P & I$\Rightarrow$\ 1,2 \par \end{fitch}$$

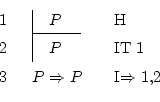
This case didn't occur before: now it seems that the left part of the sequent is empty. It means that we are not given any truth from which we can deduce $P\Rightarrow P$. Why? Because $P\Rightarrow P$ is always true, not depending on the value of $P$ or other formulas.

It's more comfortable and interesting to solve one of these demonstrations, since you start working directly on the formula which you want to achieve. But beware, since there are some absolute truths (always true) very hard and long to prove.

Note down this: whenever the left side is empty, you must start doing a hypothesis (what else could you do?).

To achieve $P\Rightarrow P$ we do as always: suppose that $P$ and try to see that $P$ is true. Since we just supposed it on the first line, we can use the iteration rule to copy it inside, and we finish the subdemonstration by using implication introduction. And we're done, in only three lines.

Remark that $P\Rightarrow P$ is true because $\blacksquare\Rightarrow\blacksquare$ and $\square\Rightarrow\square$. Well, and furthermore, remember also that $\square\Rightarrow\blacksquare$, but $\blacksquare\nRightarrow\square$.