Next: 4.9 Eliminació de la Up: 4 Les regles Previous: 4.7 Eliminació de la Contents
Aquesta és molt maca i interessant:
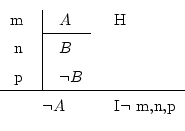
Si en suposar que ![]() , has arribat a la conclusió que són certes
, has arribat a la conclusió que són certes
![]() i
i ![]() a la vegada, no estàs perdut, ja que acabes de descobrir
una altra veritat: que no és possible que
a la vegada, no estàs perdut, ja que acabes de descobrir
una altra veritat: que no és possible que ![]() sigui cert, per tant,
que
sigui cert, per tant,
que ![]() és cert.
és cert.
Per exemple, confesso que si uso Windows, no aprofito el temps que estic amb l'ordinador. Des de fa anys sí que l'aprofito, per tant la conclusió és que no uso Windows. Per arribar a aquesta conclusió, el camí que hauries seguit (potser sense pensar-hi) és precisament el que demana aquesta regla: suposem que sí que utilitzo Windows, en aquest cas no aprofitaria el meu ordinador. Però dic que sí que ho aprofito, així que la suposició ha de ser equivocada.
A aquest procediment se l'anomena reducció a l'absurd (reductio ad absurdum): suposar quelcom per arribar a una contradicció i poder afirmar que allò suposat és fals. Va molt bé si comences suposant allò contrari al que vols demostrar: si arribes a una contradicció, ja està gairebé tot fet.
He d'avisar de que aquest és un abús de notació: resulta que
per a que quadrin els teoremes de la lògica, tota subdemostració ha
de tenir una conclusió (no dues); i en aquesta hipòtesi que
surt a la regla de dalt, no queda clar quina és la conclusió (si ![]() o
o ![]() ). La forma correcta d'escriure-ho seria usar la introducció
de la conjunció per dir que
). La forma correcta d'escriure-ho seria usar la introducció
de la conjunció per dir que ![]() , i aquesta és la conclusió
que ens fa veure que la hipòtesi inicial era errònia. Però els meus
professors s'estalviaven aquesta línia.
, i aquesta és la conclusió
que ens fa veure que la hipòtesi inicial era errònia. Però els meus
professors s'estalviaven aquesta línia.
Daniel Clemente Laboreo 2005-05-17