5.6 With subdemonstrations. $P\Rightarrow(Q\Rightarrow R)\vdash Q\Rightarrow(P\Rightarrow R)$

Things get harder. Here's the solution to $P\Rightarrow(Q\Rightarrow R)\vdash Q\Rightarrow(P\Rightarrow R)$:

$$\begin{fitch} \par P \Rightarrow (Q \Rightarrow R) \\ \par \... ...arrow (P \Rightarrow R) & I$\Rightarrow$\ 2,6 \par \end{fitch}$$

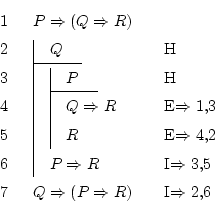
But first: here we will only use the two rules that help adding and removing implications, since it's the only operator appearing in the formulas.

We want $Q\Rightarrow(P\Rightarrow R)$, so we will have to do a hypothesis $Q$ inside of which we should prove that $P\Rightarrow R$. We now do that to simplify the problem: we open a subdemonstration at line 2. We won't close it until we discover that $P\Rightarrow R$ is true.

Now the problem is somehow easier. We just need to prove $P\Rightarrow R$, and we have two lines with two truths: the first says that $P\Rightarrow(Q\Rightarrow R)$, and the second says that $Q$.

How can we achieve the $P\Rightarrow R$? Well, as always: we must suppose $P$, and achieve that $R$ is true, in some way. Even if it doesn't seem very simple, it's what must be done, since implication introduction works that way. So we're going to open another hypothesis, now supposing $P$, and let's see if we achieve $R$. This will be a hypothesis inside a hypothesis, but there's no problem in doing that.

After writing line 3, and being inside a subsubdemonstration, we have available that $P\Rightarrow(Q\Rightarrow R)$, that $Q$, and that $P$. We must prove $R$. Now it isn't that hard, is it? If we know that $P$, we can use implication elimination on line 1, and we will get the true formula $Q\Rightarrow R$. Since $Q$ is also true (line 2), we can apply that rule again to discover that $R$.

We then see that supposing $P$ leads us to the conclusion $R$, so we can write down $P\Rightarrow R$, which is what we wanted. Now we've gone outside the subsubdemonstration, and we're only under the supposition that $Q$ is true. As we now see that this supposition implies the truth of the formula $P\Rightarrow R$, we can end this subdemonstration concluding that $Q\Rightarrow(P\Rightarrow R)$.

$Q\Rightarrow(P\Rightarrow R)$ is precisely what had to be proven, so we're finished.