Next: 5.6 With subdemonstrations. Up: 5 Explained exercises Previous: 5.4 Using iteration. Contents
This is a very useful technique. Validity of
![]() is proved with:
is proved with:
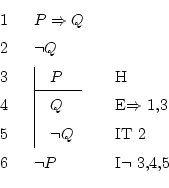
What has to be achieved here is ![]() , which is the negation
of something, so the rule which will help is the negation introduction,
also known as reduction to the absurd.
, which is the negation
of something, so the rule which will help is the negation introduction,
also known as reduction to the absurd.
The way to act will be to suppose the contrary of ![]() (which
is
(which
is ![]() ) and find a contradiction (any). Supposing
) and find a contradiction (any). Supposing ![]() will lead
us to
will lead
us to ![]() (by implication elimination), and, as we also have
(by implication elimination), and, as we also have
![]() , we can apply the rule. This
, we can apply the rule. This ![]() should be inserted
in the current subdemonstration with the iteration rule, so
that it is together with the
should be inserted
in the current subdemonstration with the iteration rule, so
that it is together with the ![]() and inside the subdemonstration.
Everything which is inside the subdemonstration is consequence of
and inside the subdemonstration.
Everything which is inside the subdemonstration is consequence of
![]() , so it is important to see that both
, so it is important to see that both ![]() and
and ![]() also
are.
also
are.
For the negation introduction, the way to justify this rule
is putting the line number of where does the (wrong) supposition start,
and the numbers of the two lines where we saw the contradiction. The
conclusion of this rule is the contrary of what we just supposed,
in this case ![]() , so we can finish the derivation here.
, so we can finish the derivation here.
This reasoning is actually made without much thinking. In words it
would be something like: ``of course that![]() , since
if it were
, since
if it were ![]() then
then ![]() , and you say that
, and you say that ![]() , so it can't
be that
, so it can't
be that ![]() ''.
''.
Daniel Clemente Laboreo 2005-05-17