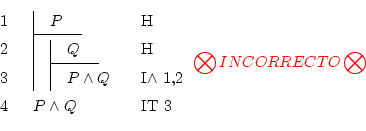6.2 Ion kopii el malatingebla subderivo

Interne de la ĉefa pruvo (kiu trairas de la unua ĝis la lasta linio) oni povas malfermi filajn derivojn (subderivojn). Interne de subderivo oni ankaŭ povas havi subsubderivon, kiu havus kiel patro la subderivo kaj kiel avo la ĉefa derivo.

Por ekzempli, jen la solvon de $A\vee B,\ A\Rightarrow C,\ \neg D\Rightarrow\neg B\vdash C\vee D$:

$$\begin{fitch} \par A \vee B \\ \par A \Rightarrow C \\ \par... ...\vee$\ 12 \\ \par C \vee D & E$\vee$\ 1,6,13 \par \end{fitch}$$

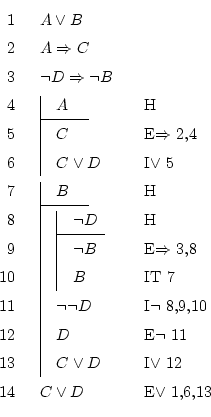
Nu, iu ajn derivo nur povas atingi formulojn el ene de si mem, el ĝia patro, el la patro de ĝia patro, el la patro de la patro de ĝia patro, ... Oni eble konas ĉi tiujn ulojn per prapatroj, do derivo povas atingi sin mem kaj siajn prapatrojn.

Ekzemple, estante ĉe linio 10, la reguloj povas uzi formulojn el la jenaj lokoj:

• el la nuna derivo (linioj 8 kaj 9, ĝisnune).
• el la derivo patra de la 8-10, tiu estas, la linio 7.
• el la derivo patra de kiu komencas en linio 7, do, linioj 1 al 3.

Neniel oni povas uzi la formulojn el la linioj 4 ĝis 6, kiu estas la derivo onkla de la nuna (frato de la patro), ĉar ĉi tiu tuta derivo estas bazita en la hipotezo ke $A$ (linio 4), kaj oni jam finis fariĝi tiun supozon.

Ĉe logika lingvo, oni diras ke formulo $A$ estas aktuala en formulo $B$ se estante en $B$ oni povas uzi $A$. Por ke ĉi tio pravu, $A$ devas esti verkita antaŭ ol $B$, kaj iu prapatro el $B$ devas esti patro de $A$.

Do, por pruvi $P\wedge Q$ vi ne rajtas fari ĉi tiel:

$$\begin{fitch} \par \fh P & H \\ \par \fa \fh Q & H \\ \par ... ...end{fitch} {\textcolor{red}{\bigotimes INCORRECTO \bigotimes}}$$