To express the relation between one action and another, there exist
some international icons. The basic operators you must know are 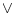 ,
,
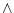 ,
, 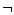 ,
, 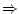 . The others are more complex, but
here I put all of them as a reference, to be able to find them if
you were searching any of them.
. The others are more complex, but
here I put all of them as a reference, to be able to find them if
you were searching any of them.
| Symbol |
It's read... |
Description |
|---|
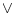 |
or |
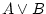 is true whenever one of the two, or both, are true. is true whenever one of the two, or both, are true. |
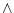 |
and |
To make 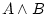 true, both true, both 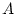 and and 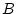 have to be true. have to be true. |
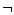 |
not |
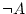 only is true when only is true when 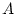 is false. is false. |
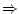 |
implies |
Shows consequence. The expression
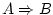 says that when says that when
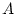 holds, so does holds, so does 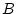 . In addition, . In addition,
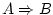 is considered
true except for the case is considered
true except for the case 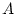 true and true and 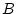 false. To understand that,
think of an false. To understand that,
think of an 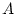 which implies which implies 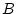 and ask yourself: is it
possible that and ask yourself: is it
possible that 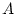 is true but not is true but not 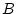 ? Anyway, don't worry about
that, it's not important right now. ? Anyway, don't worry about
that, it's not important right now. |
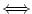 |
if and only if |
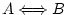 is the same as is the same as
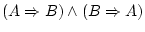 .
It means that from .
It means that from 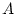 we can deduce we can deduce 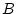 and viceversa, so they
are equivalent. and viceversa, so they
are equivalent. |
 |
false |
The empty square represents false (the binary 0). Technically,
it represents 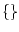 . . |
 |
true |
The filled square represents true (the binary 1). Technically,
it represents 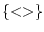 . . |
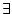 |
exists... |
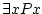 can be read there exists an can be read there exists an 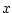 such that such that 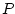 of
of 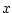 . If in our domain, we can find an element (or more) which
makes true the property . If in our domain, we can find an element (or more) which
makes true the property 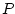 applied to that element, then the formula
is true. applied to that element, then the formula
is true. |
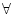 |
for all... |
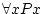 can be read for all can be read for all 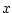 , , 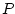 of of 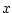 . If all
elements we are working with make the property . If all
elements we are working with make the property 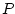 become true, then
the formula is true. become true, then
the formula is true. |
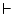 |
then |
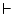 is the symbol of the sequent, which is the way of
saying ``when all this from the left happens, then it also
happens all this from the right''. There exist valid sequents, like is the symbol of the sequent, which is the way of
saying ``when all this from the left happens, then it also
happens all this from the right''. There exist valid sequents, like
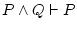 or like or like
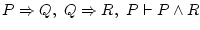 .
But there are also invalid ones, like .
But there are also invalid ones, like
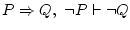 .
The objective of natural deduction is to prove that a sequent is valid. .
The objective of natural deduction is to prove that a sequent is valid. |
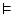 |
valid |
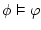 means that means that 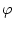 is logical consequence
of is logical consequence
of 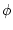 , but when one writes , but when one writes 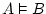 , what we mean is that
the sequent , what we mean is that
the sequent 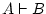 is valid, that is, we could somehow prove
it, and now is considered true for any interpretation of the predicate
symbols. is valid, that is, we could somehow prove
it, and now is considered true for any interpretation of the predicate
symbols. |
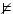 |
invalid |
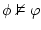 means that means that 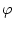 is not logical consequence
of is not logical consequence
of 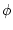 . If you can find a series of values (model) which
make . If you can find a series of values (model) which
make 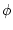 true but true but 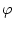 false, then invalidity is proven. false, then invalidity is proven. |
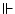 |
satisfiable |
A set of formulas is satisfiable if there exists a series of values
(model) which can make all of them true at the same time. |
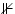 |
unsatisfiable |
A set of formulas is unsatisfiable if there isn't any combination
of variables (model) which can make all of them become true
at the same time. |
![]() ,
,
![]() ,
, ![]() ,
, ![]() . The others are more complex, but
here I put all of them as a reference, to be able to find them if
you were searching any of them.
. The others are more complex, but
here I put all of them as a reference, to be able to find them if
you were searching any of them.