Next: 6.4 Finish inside a Up: 6 Wrong things Previous: 6.2 Iterate something from Contents
When I wrote the definitions of the rules, I used the letters ![]() and
and ![]() , but these can represent any expression.
, but these can represent any expression.
For instance, here we do negation introduction, in which -following
the rule- we suppose some formula ![]() , attain a contradiction, and
we conclude
, attain a contradiction, and
we conclude ![]() , so, the original formula, but negated. Let's
see:
, so, the original formula, but negated. Let's
see:
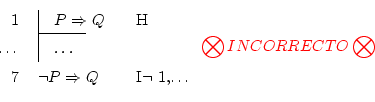
I think it's clear that the ![]() which appears in the rule represents
to
which appears in the rule represents
to
![]() in this example. The problem comes when we do
the
in this example. The problem comes when we do
the ![]() . The negation of
. The negation of
![]() is not
is not
![]() ,
but
,
but
![]() . It's necessary that parenthesis because
if not present, the negation affects only
. It's necessary that parenthesis because
if not present, the negation affects only ![]() .
.
If you don't know when to put parenthesis, always put them, and then
try to remove the unneeded ones. For instance, if you must write that
![]() implies
implies ![]() , put parenthesis around each
expression and thus write
, put parenthesis around each
expression and thus write
![]() .
This way, there are absolutely no errors. Now learn when is it possible
to remove parenthesis, and take away all that you can. In this case,
both can be suppressed and it remains
.
This way, there are absolutely no errors. Now learn when is it possible
to remove parenthesis, and take away all that you can. In this case,
both can be suppressed and it remains
![]() .
.
Daniel Clemente Laboreo 2005-05-17