6.1 Introduction and elimination of ``what it would be nice to have''

The rules like introduction and elimination are not to allow you writing anything you want, but to help you using or creating a formula with a concrete operator.

That's why, if you have $P$, you can't say ``now I do negation introduction and get $\neg P$, which is what I needed''. There are some requisites for each rule, and if you don't fulfill them, you can't apply that rule.

For instance: the rule implication elimination doesn't allow to use the formulas in the first line this way:

$$\begin{fitch} \par P \Rightarrow Q \wedge R \\ \par Q \wedge... ...end{fitch} {\textcolor{red}{\bigotimes INCORRECTO \bigotimes}}$$

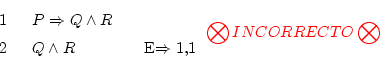
To be able to do this, we would need to be sure that $P$ is always true; then we could apply the rule, correctly writing the line numbers.