Next: 5.5 Reduction to the Up: 5 Explained exercises Previous: 5.3 Starting to make Contents
This is a short one:
![]() . Solution:
. Solution:
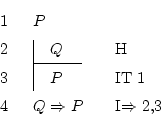
The way is clear: we have to suppose ![]() , and finally see that, in
that case,
, and finally see that, in
that case, ![]() is true. The trick:
is true. The trick: ![]() is always true, whether we
suppose
is always true, whether we
suppose ![]() or not.
or not.
We must use implication introduction, but this needs a hypothesis, and, some lines below, the result of the supposition. Only then we can close the hypothesis.
So after opening it (line 2), we must do something to write down that
![]() . Since we already have it written in line 1, we simply put
. Since we already have it written in line 1, we simply put ![]() again and justify it with
again and justify it with ![]() , which means ``I copied
this from line 1''. The
, which means ``I copied
this from line 1''. The ![]() is for iteration.
is for iteration.
We now fulfill the requirements to apply the rule, so we apply it, closing the subdemonstration, and we've ended.