5.1 A very simple one. $P,\ P\Rightarrow Q\vdash P\wedge Q$

The solution to $P,\ P\Rightarrow Q\vdash P\wedge Q$ is:

$$\begin{fitch} \par P \\ \par P \Rightarrow Q \\ \par Q & E$... ...ow$\ 2,1 \\ \par P \wedge Q & I$\wedge$\ 1,3 \par \end{fitch}$$

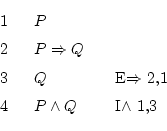
Here we won't have to think much, we just have to use correctly the rules and their justifications.

Firstly, understand what has been told to us: they say that now happen two things, the first is that $P$ and the second is that $P\Rightarrow Q$ (they are the two formulas written to the left of the $\vdash$). These two things we will note, one on each line, since at this demonstration they will always be true (liking it or not).

The goal of this demonstration is to know that $P\wedge Q$ is also true, as we have been told that when $P$ and $P\Rightarrow Q$ are true, then $P\wedge Q$ also is, and we want to check if that's right. Finally we achieved it, since on the last line we see the $P\wedge Q$ written.

But how do we start? Remember where do we want to head to. If $P\wedge Q$ has to be true, then both $P$ and $Q$ should be true; let's attempt to prove that they really are.

$P$ is true, since they said so, and we have it written on line 1.

But we weren't told that $Q$ was true. What do we know about $Q$? Searching it on lines 1 and 2, the only we know about $Q$ is that it's true when happens $P$ (that's what says line 2). But $P$ is true, so we can use one of the rules to deduce $Q$ from the $P\Rightarrow Q$ and $P$. Remark what is the most important change when we go from $P\Rightarrow Q$ to $Q$: we stopped using the implication symbol; so the rule we will need is the one called implication elimination.

To use this rule, we look at its definition, and see that we have to write in a new line $Q$, and as a justification $E\Rightarrow\ 2,1$ needs to be written. The $E$ is from elimination, the $\Rightarrow$ means implication, the first number is the one from the line which does contain the implication ( $P\Rightarrow Q$), and the second number is from the line which has the known truth ($P$). It's incorrect to write them reversed ( $E\Rightarrow\ 1,2$), since the definition of the rule says that the line which has the implication should be cited first.

We have just applied the rule, and now we know three truths: $P$, $P\Rightarrow Q$, and $Q$. They are all equally true. Now we're nearer to our objective, $P\wedge Q$, since we know that $P$ and $Q$ are true, so $P\wedge Q$ also has to be true (it's obvious). In the formula we search there's a conjunction sign ($\wedge$) which we don't have, so we need to use the conjunction introduction to be able to say that $P\wedge Q$ is true because $P$ is and also $Q$. As a justification we write $I\wedge\ 1,3$ (the line where it says $P$, and the one which says $Q$). Don't put $I\wedge\ 3,1$, that would be to affirm that $Q\wedge P$, which is not what we're trying to prove.

Then we know 4 truths: $P$, $P\Rightarrow Q$, $Q$, and $P\wedge Q$. We could continue finding more things which are true, but we've already finished, since we had been told to prove that $P\wedge Q$ is true, and we just achieved that (in line 4). So that will be the last line, and we don't have to write anything else.

Ah, and an example of this derivation, but with words: ``now it's summer, and in summer it's warm. That's why now it's summer and it's warm''.