4.1 Iteration

This is a very simple rule:

$$\begin{fitch*} \par n & A \\ \par \hline \par & A & IT n \par \end{fitch*}$$

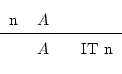
Well, I know, written like this is a bit strange, but I put it this way to make it useful as the definition of the rule. What is contained in the above formulation is that if on line number $n$ we have written $A$ (whatever expression it is) then we have the option to write again $A$, but in the current line, and to justify that, we must write at the right $IT\ n$.

So, why would we want that? Well, for the moment, for nothing, but it will have its utility when we start working with hypothesis. Since a hypothesis is closed, all rules will have to work with formulas inside the hypothesis. If one of the formulas we want is just outside this hypothesis, we can copy it herein by using this rule called iteration.

Some people think that it's not necessary to waste a line this way, but it's a lot clearer when this rule is used. What isn't allowed is using it only to ``bring nearer'' some formula which is several lines far away: it isn't necessary to rewrite a line if we have it already written in the current derivation.