Next: 5.6 Amb subdemostracions. Up: 5 Exercicis explicats Previous: 5.4 Usant la iteració. Contents
Aquesta és una tècnica molt útil. La validesa de
![]() es demostra amb:
es demostra amb:
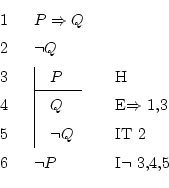
A on s'ha d'arribar és a ![]() , que és la negació d'alguna
cosa, per això s'haurà d'utilitzar la regla de introducció
de la negació, coneguda per reducció a l'absurd.
, que és la negació d'alguna
cosa, per això s'haurà d'utilitzar la regla de introducció
de la negació, coneguda per reducció a l'absurd.
La forma de fer-ho serà suposar el contrari de ![]() (que és
(que és ![]() )
i arribar a una contradicció. En suposar
)
i arribar a una contradicció. En suposar ![]() arribarem a
arribarem a ![]() (per
eliminació de la implicació), i com que també tenim
(per
eliminació de la implicació), i com que també tenim ![]() ,
podem aplicar la regla. Aquest
,
podem aplicar la regla. Aquest ![]() l'haurem de repetir a dintre
la subdemostració amb la regla d'iteració, per a que estigui
junt amb la
l'haurem de repetir a dintre
la subdemostració amb la regla d'iteració, per a que estigui
junt amb la ![]() però també dins de la subdemostració. Tot
el que hi ha a dins de la subdemostració és conseqüència de
però també dins de la subdemostració. Tot
el que hi ha a dins de la subdemostració és conseqüència de ![]() ,
així que és important veure que tant
,
així que és important veure que tant ![]() com
com ![]() ho són.
ho són.
Per a la introducció de la negació, la forma de justificar
la regla és posant el número de línia on comença la suposició (errònia),
i els números de les dues línies on hem vist la contradicció. La conclusió
d'aquesta regla és el contrari d'allò que s'havia suposat, en aquest
cas ![]() , per tant ja podem acabar el procediment.
, per tant ja podem acabar el procediment.
Aquest raonament normalment el fem sense pensar-hi gaire. En paraules
seria semblant a: ``és clar que ![]() , perquè si fos
, perquè si fos
![]() llavors
llavors ![]() , i em diuen que
, i em diuen que ![]() , així que no pot ser
, així que no pot ser ![]() ''.
''.
Daniel Clemente Laboreo 2005-05-17