5.11 Éste parece sencillo. $\vdash P\vee\neg P$

A ver si $\vdash P\vee\neg P$ es tan obvio como dicen:

$$\begin{fitch} \par \fh \neg (P \vee \neg P) & H \\ \par \fa ... ...\ 1,5,10 \\ \par P \vee \neg P & E$\neg$\ 11 \par \end{fitch}$$

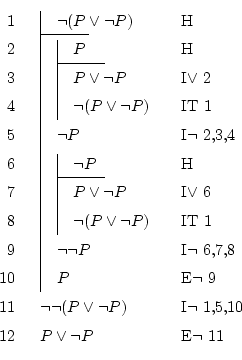
Uno de los más simples y largos que he encontrado. Parece que no sea necesario demostrarlo, porque todo el mundo sabe que entre ``hoy es jueves'' y ``hoy no es jueves'', una de las dos es cierta (no pueden ser falsas las dos a la vez).

Podríamos empezar pensando en el método de prueba por casos, porque de $P$ podemos deducir $P\vee\neg P$, y de $\neg P$ podemos deducir $P\vee\neg P$, o sea, la misma fórmula. Pero esto no sirve de nada, porque la regla de prueba por casos es la de eliminación de la disyunción, y no tenemos ninguna disyunción por eliminar; de hecho, tampoco tenemos la fórmula cierta $A\vee B$ tal que $A\Rightarrow C$ y $B\Rightarrow C$, como pide la regla. En realidad, no tenemos ninguna fórmula que sepamos que sea cierta (el lado izquierdo del secuente está vacío).

Sabemos que hay que empezar con una hipótesis (no hay otra alternativa). Como queda bastante claro que $P\vee\neg P$ es cierto, también puede parecer fácil demostrar que su contrario, $\neg(P\vee\neg P)$, es falso. Así que usaremos la reducción al absurdo: haciendo esa suposición en la línea 1, hay que intentar llegar a una contradicción, la que sea.

Yo me propuse llegar a la contradicción $\neg P$ y $P$. Pero no tenemos ninguna de esas fórmulas; ¿cómo las sacamos? Pues volvemos a hacer reducción al absurdo: para ver que $\neg P$, vamos a suponer que $P$ para llegar a una contradicción. Como otras veces, va muy bien aprovechar las posibilidades que da la introducción de la disyunción: al suponer que $P$, podremos convertirlo en $P\vee\neg P$ para buscar la contradicción. Como tenemos el $\neg(P\vee\neg P)$ arriba del todo, lo podemos usar para acabar demostrando que $\neg P$. Lo mismo haremos para demostrar que $P$, pero esta vez suponiendo $\neg P$.

Al haber llegado a $P$ y $\neg P$ después de suponer $\neg(P\vee\neg P)$, se ve que esta fórmula no puede ser cierta, así que su negación, $\neg\neg(P\vee\neg P)$, lo es. Por eliminación de la negación, nos queda la fórmula que buscamos: $P\vee\neg P$.

Lo he hecho de esta manera para que quedara bastante simétrico, pero se puede hacer más corto buscando otra contradicción, por ejemplo $P\vee\neg P$ y $\neg(P\vee\neg P)$. Quedaría así:

$$\begin{fitch} \par \fh \neg (P \vee \neg P) & H \\ \par \fa ... ...g$\ 1,6,7 \\ \par P \vee \neg P & E$\neg$\ 8 \par \end{fitch}$$