5.7 Uno de prueba por casos. $P\vee(Q\wedge R)\vdash P\vee Q$

Habrá que usar la regla más complicada: la eliminación de la disyunción. $P\vee(Q\wedge R)\vdash P\vee Q$ solucionado:

$$\begin{fitch} \par P \vee (Q \wedge R) \\ \par \fh P & H \\ ... ...I$\vee$\ 5 \\ \par P \vee Q & E$\vee$\ 1,3,6 \par \end{fitch}$$

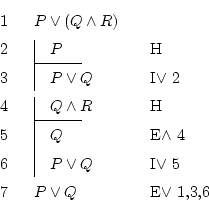
Ya conoces las reglas, así que explico la forma de pensar de un humano que no entienda de deducción natural pero que piense un poquito:

Necesitamos comprobar que $P\vee Q$ es cierto siempre. La expresión de la izquierda, $P\vee(Q\wedge R)$, se puede cumplir por dos motivos:

• si se cumple porque $P$ es cierto, entonces $P\vee Q$ es cierto.
• si se cumple porque $Q\wedge R$ es cierto, es que $Q$ y $R$ son ciertas, así que $P\vee Q$ es cierto gracias a $Q$.

O sea, que de cualquier manera, $P\vee Q$ es cierto.

Pues ahora lo único que hay hacer es traducir a lenguaje lógico, siguiendo el mismo orden en el que se ha pensado, y yendo poco a poco.

Se empieza demostrando un camino, luego el otro, y por último se aplica la regla de eliminación de la disyunción. Para justificarla hay que escribir la línea donde está la disyunción, y las dos líneas de dentro de cada subdemostración donde se vea que tanto al suponer una cosa como al suponer la otra, el resultado es el mismo.

Fíjate que, aunque averigüemos que $P\Rightarrow P\vee Q$ y que $Q\wedge R\Rightarrow P\vee Q$, no hace falta usar la introducción de la implicación para dejar escrito eso.

Lo más complicado de la prueba por casos suele ser decidir qué expresión vas a demostrar en ambos casos. ¡Tiene que ser la misma para los dos casos!