Next: 5.6 Con subdemostraciones. Up: 5 Ejercicios explicados Previous: 5.4 Usando la iteración. Contents
Ésta es una técnica muy útil. La validez de
![]() se demuestra con:
se demuestra con:
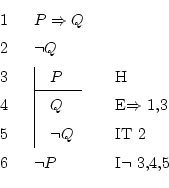
A lo que hay que llegar es a ![]() , que es la negación de
algo, por eso habrá que usar la regla de introducción de la
negación, conocida como reducción al absurdo.
, que es la negación de
algo, por eso habrá que usar la regla de introducción de la
negación, conocida como reducción al absurdo.
La forma de hacer esto será suponer lo contrario de ![]() (que
es
(que
es ![]() ) y llegar a una contradicción. Al suponer
) y llegar a una contradicción. Al suponer ![]() llegaremos
a
llegaremos
a ![]() (por eliminación de la implicación), y como también
tenemos que
(por eliminación de la implicación), y como también
tenemos que ![]() , podremos aplicar la regla. Este
, podremos aplicar la regla. Este ![]() habrá
que meterlo dentro de la subdemostración con la regla de iteración,
para que esté junto con la
habrá
que meterlo dentro de la subdemostración con la regla de iteración,
para que esté junto con la ![]() y dentro de la subdemostración.
Todo lo que hay dentro de la subdemostración es consecuencia de
y dentro de la subdemostración.
Todo lo que hay dentro de la subdemostración es consecuencia de ![]() ,
así que es importante ver que tanto
,
así que es importante ver que tanto ![]() como
como ![]() lo son.
lo son.
Para la introducción de la negación, la forma de justificar
la regla es poniendo el número de línea donde empieza la suposición
(errónea), y los números de las dos líneas donde hemos visto la contradicción.
La conclusión de esta regla es lo contrario de lo que se había supuesto,
en este caso ![]() , por lo que se acaba el procedimiento.
, por lo que se acaba el procedimiento.
Este razonamiento se suele hacer sin pensar. En palabras sería algo
así: ``claro que ![]() , porque si fuera
, porque si fuera ![]() entonces
entonces
![]() , y me dicen que
, y me dicen que ![]() , así que no puede ser
, así que no puede ser ![]() ''.
''.
Daniel Clemente Laboreo 2005-05-17