5.11 Tiu ŝajnas facila. $\vdash P\vee\neg P$

Ĉu $\vdash P\vee\neg P$ estas tiom facila?

$$\begin{fitch} \par \fh \neg (P \vee \neg P) & H \\ \par \fa ... ...\ 1,5,10 \\ \par P \vee \neg P & E$\neg$\ 11 \par \end{fitch}$$

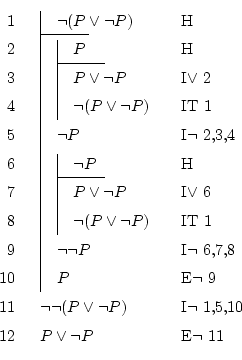
Unu el la plej simplaj kaj longaj kiuj mi trovis. Ŝajnas eĉ ne necese pruvadi tion, ĉar iu ajn scias ke el la du aĵojn ``hodiaŭ estas ĵaŭdo'' kaj ``hodiaŭ ne estas ĵaŭdo'', unu el ili estas certa (ne eblas ke ambaŭ estu falsaj samtempe).

Oni povus unue pensi en la rimedon de provo per okazoj, ĉar el $P$ eblas eltiri $P\vee\neg P$, kaj el $\neg P$ eltiri $P\vee\neg P$, do, la saman formulon. Sed tio malutilas, ĉar derivregulo de provo per okazoj estas elaŭigo kaj oni mankas iun aŭon por eligi; fakte, oni nek havas la certan formulon $A\vee B$ tiel ke $A\Rightarrow C$ kaj $B\Rightarrow C$, kiel la regulo bezonas. Plej fakte, oni havas neniun formulon kies certecon oni povas aserti (la maldekstra parto de la derivo estas malplena).

Oni scias ke ĉe la komenco, hipotezon devas fari (ĉar ne estas alia vojo). Estas ``sufiĉe'' klara por ni ke $P\vee\neg P$ certas, do verŝajne ĝian kontraŭan, $\neg(P\vee\neg P)$, estos facile pruvebla falsa. Do oni uzos redukton al absurdo: supozinte tion ĉe linio 1, oni devas atingi memkontraŭdiron, iu ajn.

Mi celis atingi kontraŭdiron $\neg P$ kaj $P$. Tamen, oni mankas tiujn formulojn; kie ni trovigos ilin? Nu, eblas refari redukton al absurdo: por ekvidi $\neg P$, supozu $P$ por atingi memkontraŭdiron. Kiel antaŭe, estas utilege profiti eblojn de kunaŭigo: supozinte $P$, oni povas ŝanĝigi ĝin al $P\vee\neg P$ por serĉi kontraŭdiron. Ĉar oni havas la $\neg(P\vee\neg P)$ tute supre, oni rajtas uzi ĝin por fine pruvi $\neg P$. Same oni faras por atingi $P$, sed tiuokaze supozante $\neg P$.

Ricevite $P$ kaj $\neg P$ post la supozado de $\neg(P\vee\neg P)$, oni vidas ke tiu formulo maleblas certi, do ĝia nego, $\neg\neg(P\vee\neg P)$, ja certas. Per elnegigo, fine estas trovita serĉatan formulon: $P\vee\neg P$.

Mi agis tiel por igi la skemon iom simetria, sed oni ja povas solvi la problemon per malpliaj paŝoj serĉante alian memkontraŭdiron, ekzemple $P\vee\neg P$ kaj $\neg(P\vee\neg P)$. Tiel ĝi restus:

$$\begin{fitch} \par \fh \neg (P \vee \neg P) & H \\ \par \fa ... ...g$\ 1,6,7 \\ \par P \vee \neg P & E$\neg$\ 8 \par \end{fitch}$$