Next: 7.2 Rules about quantifiers Up: 7.1 Rules about truth Previous: 7.1.1 Truth introduction Contents
A funny one:
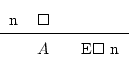
Explanation: if we achieved the conclusion that ![]() is true,
then we have already achieved a state where we can invent anything
and affirm that it's true; at least, as true as the idea of
is true,
then we have already achieved a state where we can invent anything
and affirm that it's true; at least, as true as the idea of ![]() (false) being true.
(false) being true.
This rule is called ex falso quodlibet sequitur, something like ``from false can follow anything''.