Next: 6.3 Misplace parenthesis Up: 6 Wrong things Previous: 6.1 Introduction and elimination Contents
Inside the main demonstration (which goes from the first line to the last), we can open child demonstrations (subdemonstrations). Inside any subdemonstration we can also have a subsubdemonstration, which would have as father the subdemonstration and as grandfather the main demonstration.
To understand this, here is the solved example
![]() :
:
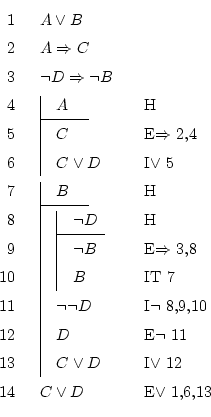
Well, any demonstration can only access the formulas from inside itself, inside its father, inside the father of its father, inside the father of the father of its father, ... All these are called ancestors, so: a demonstration can access itself and its ancestors.
For this reason, it we are on line 10, the derivation rules can use formulas from the following places:
In logical language, one says that a formula ![]() is actual
at formula
is actual
at formula ![]() if being in
if being in ![]() we can use
we can use ![]() . For this to be true,
. For this to be true,
![]() must have been written before
must have been written before ![]() , and some ancestor of
, and some ancestor of ![]() must be father of
must be father of ![]() .
.
So, to prove ![]() we can't do this:
we can't do this:
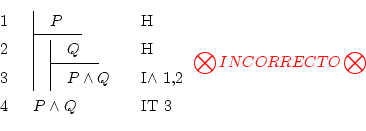
Daniel Clemente Laboreo 2005-05-17