5.3 Starting to make suppositions. $P\Rightarrow Q,\ Q\Rightarrow R\vdash P\Rightarrow Q\wedge R$

This one, $P\Rightarrow Q,\ Q\Rightarrow R\vdash P\Rightarrow Q\wedge R$, is more interesting:

$$\begin{fitch} \par P \Rightarrow Q \\ \par Q \Rightarrow R \... ... \Rightarrow Q \wedge R & I$\Rightarrow$\ 3,6 \par \end{fitch}$$

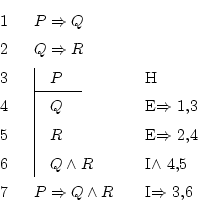
Note the following details:

• We aren't told any information about what does happen now (we don't have formulas like $P$, or $Q\wedge R$, etc.). They only say things like that if happened $P$, then $Q$ would also happen.
• In the same way, what we must prove is not that just now happens something, but that if it happened $P$, then $Q$ and $R$ would be true.
• $P\Rightarrow Q\wedge R$ is an implication (something implies something), because operator $\Rightarrow$ has less priority than $\wedge$. It's a big error to understand that formula as $(P\Rightarrow Q)\wedge R$.

As the formula we want is an implication ( $P\Rightarrow Q\wedge R$), we will have to use the implication introduction, but this rule needs having a subdemonstration (look it up at its definition).

It isn't hard to understand why: $P\Rightarrow Q\wedge R$ says that if it happens $P$, then happens $Q\wedge R$, so the first we should do is to suppose that $P$ really does happen. Then we will have to discover that, in this case when $P$ is true, it is also true $Q\wedge R$. When we get that, we will apply the rule and write everything politely: $P\Rightarrow Q\wedge R$.

For that reason, at line 3 we make an hypothesis (justified by the $H$ at the right): suppose that $P$ is true. Now we're starting a subdemonstration, where we will be able to use the truths that were on the father demonstration (lines 1 and 2 in this case), and also we can use $P$ as if it were another truth.

We made this hypothesis aiming to know that $Q\wedge R$, so we deduce it similarly to the previous exercises. Notice that we use truths from inside and from outside the subdemonstration, and also that, while we haven't finished it, that vertical line to the left must be put.

In line 6 we now have $Q\wedge R$, which is what we were looking for. Using the implication introduction rule, we can go outside this subdemonstration by saying that if the hypothesis is true, then what we deduced from it also is true. We stop putting that vertical line, since $P\Rightarrow Q\wedge R$ is always true (it doesn't depend on whether $P$ is true or not). The justification we used, $I\Rightarrow\ 3,6$, says that 3 is the line where we made the supposition, and 6 the line where we discovered something interesting which happens when we make that supposition.

$P\Rightarrow Q\wedge R$ is what we wanted, so we have finished. We finish as always, since we're outside any subdemonstration.