Next: 4.9 Negation elimination Up: 4 The derivation rules Previous: 4.7 Disjunction elimination Contents
This one is nice and interesting:
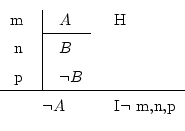
If after supposing ![]() , you achieved the conclusion that both
, you achieved the conclusion that both ![]() and
and ![]() are true, you're not lost, since you just discovered
another truth: that it's not possible for
are true, you're not lost, since you just discovered
another truth: that it's not possible for ![]() to be true, that's
it,
to be true, that's
it, ![]() it's true.
it's true.
For instance, I confess that if I use Windows, I don't profit the time I am with my computer. Since some years, I do profit it, so the conclusion is that I don't use Windows. To achieve that conclusion, the path that you would follow (maybe without thinking) is precisely the one that this rule needs: suppose that I do use Windows, in that case I wouldn't profit my computer. But I said that I do profit it, so that supposition must be wrong.
This procedure is called reduction to the absurd (reductio ad absurdum): suppose something to achieve a contradiction and be able to assert that what we supposed is false. It's specially useful if you start supposing the contrary of what you want to prove: if any contradiction can be discovered, then it's almost all done.
I should note that this is an abuse of notation: following
all the laws of logic, it happens that each subdemonstration needs
one conclusion (not two); and at the above hypothesis, it's
not clear which one is the conclusion (![]() or
or ![]() ?). The correct
way to write it would be using conjunction introduction to
say that
?). The correct
way to write it would be using conjunction introduction to
say that ![]() , and this one is the conclusion which shows
the wrongness of the initial hypothesis. But my teachers didn't write
that line.
, and this one is the conclusion which shows
the wrongness of the initial hypothesis. But my teachers didn't write
that line.
Daniel Clemente Laboreo 2005-05-17