4.4 Implication introduction

This is more interesting, since it allows doing something useful with hypothesis (those subdemonstrations which have a vertical bar to the left). It's:

$$\begin{fitch*} \par m & \fh A & H \\ \par n & \fa B \\ \par... ...\par & A \Rightarrow B & I$\Rightarrow$\ m,n \par \end{fitch*}$$

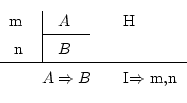
And what it does mean is that if we supposed something (call it $A$), and we just discovered (by using the rules) that supposing $A$ made true $B$ (whatever it is), then we have something clear: we can't assure that $B$ always is true, but we can assure that $A$ implies $B$, which is written $A\Rightarrow B$.

This allows us to end the subdemonstration and continue working with what we were doing before. Remember that you can't finish natural deduction inside a subdemonstration.