4.2 Conjunction introduction

The conjunction (that's the and) can be created easily:

$$\begin{fitch*} \par m & A \\ \par n & B \\ \par \hline \par & A \wedge B & I$\wedge$\ m,n \par \end{fitch*}$$

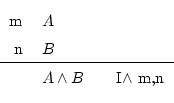
You should be able to understand the meaning of figures like this one. When we put a long horizontal line, normally it's to separate the premises (top) from the conclusion (bottom). Premises are conditions which must be fulfilled in order to apply the rule, and conclusion (or resolvent) is the result of the application of the rule.

This rule says that if on one line we have written a truth, and on another line we have another one, also true, then we can write in just a line that both things are true. We must then note to the right the lines from where we picked the first and the second formulas.

This is pretty logic, isn't it? if we know that really it's raining, and that it's true that now it's sunny, then there's no problem in saying that it's raining and sunny (yes, at the same time). If something feels strange, it's not our fault; blame the one who told us that it's raining or it's sunny.

Remark that picking the lines reversed, you can obtain $B\wedge A$, and picking the same line you can achieve $A\wedge A$ and $B\wedge B$, which are also true.