5.13 Éste me lo pusieron en un examen. $A\vee B,\ A\Rightarrow C,\ \neg D\Rightarrow\neg B\vdash C\vee D$

En el examen final de ILO me pusieron $A\vee B,\ A\Rightarrow C,\ \neg D\Rightarrow\neg B\vdash C\vee D$, y me pasé mucho, mucho rato hasta que lo conseguí:

$$\begin{fitch} \par A \vee B \\ \par A \Rightarrow C \\ \par... ...\vee$\ 12 \\ \par C \vee D & E$\vee$\ 1,6,13 \par \end{fitch}$$

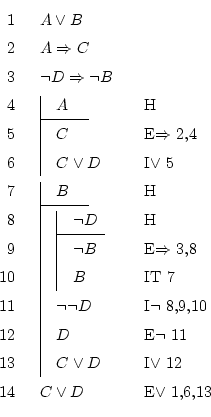
Fíjate en que el resultado que buscamos, $C\vee D$, es una disyunción. Como ya conoces la introducción de la disyunción, podrías buscar simplemente que $C$, y luego utilizar esta regla para sacar $C\vee D$. Si no encontraras que $C$ es cierta, pues podrías probar con $D$, porque si $D$ es cierta entonces $C\vee D$ lo es y ya hemos acabado.

Desgraciadamente, $C$ no es cierta siempre, y $D$ tampoco es cierta siempre (en cambio $C\vee D$ sí que lo es siempre, y eso es lo que queremos demostrar). Después de comprobar esto, habrá que buscar otro método que trabaje con las dos fórmulas $C$ y $D$, a la vez, porque parece que si cogemos una sola sin mirar la otra, no proporciona mucha información.

Para usar el $A\vee B$ habrá que usar la prueba por casos. Intentaremos llegar a que tanto $A$ como $B$ llevan a $C\vee D$, porque si lo conseguimos ya habremos acabado.

$A$ implica $C$, y si $C$ es cierto también lo es $C\vee D$, así que $A$ implica $C\vee D$.

Con $B$, lo que sabemos no la relaciona con la $C$ sino con la $D$. Queremos $C\vee D$. Difícilmente conseguiremos que $C\vee D$ se cumpla gracias a $C$, así que intentaremos que sea $D$ la cierta. Para ello, usamos reducción al absurdo: supongamos que $D$ es falso, entonces se cumple $\neg B$ por la fórmula de la línea 3. Pero estábamos dentro de la suposición de que $B$ era cierto, así que nuestra hipótesis $\neg D$ no puede ser cierta, luego $D$ es cierta, y por tanto $C\vee D$ también.

Como $A\vee B$ es cierto, y los dos caminos nos llevan a $C\vee D$, acabamos viendo que $C\vee D$ siempre es cierto.

Si tienes práctica trabajando con fórmulas lógicas, habrás visto que $\neg D\Rightarrow\neg B$ es $B\Rightarrow D$. Eso simplifica mucho el problema y ayuda a entenderlo antes. De todas formas, no puedes cambiar $\neg D\Rightarrow\neg B$ por $B\Rightarrow D$ directamente, sino que hay que hacerlo paso a paso.