5.1 Uno muy sencillo. $P,\ P\Rightarrow Q\vdash P\wedge Q$

La solución a $P,\ P\Rightarrow Q\vdash P\wedge Q$ es:

$$\begin{fitch} \par P \\ \par P \Rightarrow Q \\ \par Q & E$... ...ow$\ 2,1 \\ \par P \wedge Q & I$\wedge$\ 1,3 \par \end{fitch}$$

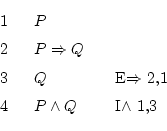
Aquí no hay que pensar mucho, simplemente hay que usar bien las reglas y justificaciones.

Lo primero, entender lo que nos han dicho: nos dicen que ahora pasan dos cosas, la primera es que $P$ y la segunda es que $P\Rightarrow Q$ (son las dos fórmulas que hay a la izquierda del $\vdash$). Estas dos cosas nos las tenemos que apuntar, una en cada línea, porque en esta demostración serán siempre ciertas (nos guste o no).

El objetivo de esta demostración es saber que $P\wedge Q$ también es cierto, porque nos han contado que cuando $P$ y $P\Rightarrow Q$ son ciertos, entonces $P\wedge Q$ también, y queremos comprobar si es verdad. Al final se ha conseguido, porque en la última línea sale el $P\wedge Q$ escrito.

¿Cómo seguimos ahora? Hay que fijarse en a dónde queremos llegar. Si $P\wedge Q$ tiene que ser cierto, entonces tanto $P$ como $Q$ tendrán que ser ciertos; vamos a preocuparnos por demostrar que lo son.

$P$ es cierto, porque nos lo han dicho, y lo tenemos apuntado en la línea 1.

Pero no nos han dicho que $Q$ lo sea. ¿Qué han dicho sobre $Q$? Buscándola en las líneas 1 y 2, lo único que conocemos es que $Q$ es cierta cuando pasa $P$ (lo pone en la 2). Y como $P$ es cierta, podemos usar una de las reglas para deducir $Q$ a partir del $P\Rightarrow Q$ y de $P$. Fíjate en qué es lo más importante que ha pasado al cambiar de $P\Rightarrow Q$ a $Q$: se ha dejado de usar el símbolo de la implicación; así que la regla que necesitamos se llama eliminación de la implicación.

Para usar esta regla, miramos la definición, y vemos que tenemos que poner en una nueva línea la $Q$, y como justificación hay que escribir $E\Rightarrow\ 2,1$. La $E$ viene de eliminación, el $\Rightarrow$ es por implicación, el primer número es el de la línea que contiene implicación ( $P\Rightarrow Q$), y el segundo número es el de la línea que contiene la verdad conocida ($P$). Es incorrecto ponerlos al revés ( $E\Rightarrow\ 1,2$), porque en la definición de la regla pone que la línea que tiene la implicación tiene que ser citada en primer lugar.

Ya hemos aplicado la regla, y ya sabemos tres cosas que son ciertas: que $P$, que $P\Rightarrow Q$, y que $Q$. Todas son igual de ciertas. Ahora estamos más cerca del objetivo, $P\wedge Q$, porque ya sabemos que $P$ y $Q$ son ciertas, así que $P\wedge Q$ también tiene que serlo (es obvio). En la fórmula que buscamos hay un signo de conjunción ($\wedge$) que no tenemos, así que hay que usar la introducción de la conjunción para afirmar que $P\wedge Q$ es cierto porque $P$ lo es y $Q$ también. Como justificación ponemos $I\wedge\ 1,3$ (la línea donde pone que $P$, y la que pone que $Q$). No vale poner $I\wedge\ 3,1$, eso sería para asegurar que $Q\wedge P$, que no es lo que piden demostrar.

Entonces ya sabemos que 4 cosas son ciertas: $P$, $P\Rightarrow Q$, $Q$, y $P\wedge Q$. Podríamos seguir descubriendo más cosas ciertas, pero es que ya hemos acabado, porque nos pedían demostrar que $P\wedge Q$ es cierto y ya lo hemos conseguido (en la línea 4). Por lo tanto, ésta será la última línea, y no hay que escribir nada más.

Ah, un ejemplo de esto con palabras: ``ahora es verano, y en verano hace calor. Por eso ahora es verano y hace calor''.